因果观念新革命？万字长文，解读复杂系统背后的暗因果

导读：一直以来，人们对因果的理解和处理都止步于线性因果关系。最近PNAS上发表了两篇探讨因果推断的论文，通过考察金融市场要素之间的潜藏的交互作用，定义了一种新型因果：暗因果，并发展出一种基于符号动力学最近邻域相空间重构的方法，对各种因果关系了进行分离和计算。

导语

一直以来，人们对因果的理解和处理都止步于线性因果关系。最近PNAS上发表了两篇探讨因果推断的论文，通过考察金融市场要素之间的潜藏的交互作用，定义了一种新型因果：暗因果，并发展出一种基于符号动力学最近邻域相空间重构的方法，对各种因果关系了进行分离和计算。在对各种复杂系统进行测试之后，他们证明这种方法在重构因果关系的能力上具有相当大的准确度，胜过几乎所有流行的因果推断方法。

目录

一、 因果观念的变迁

二、 暗因果关系的发现

三、 计算时空邻域与因果模式矩阵

四、 应用例子与效果对比

五、 因果之路走向何方

干燥的空气，炙烤着山下的溪谷，一阵雷暴之后，旁边的森林蹿起一场漫天大火。

一时间森林里的动物们，无论老虎还是狐狸，兔子还是蜂猴，都仿佛收到了天上某种信号，纷纷逃窜[1]。距今十万年前丹尼索瓦人的穴洞边上口，这一切被一个小女孩看在眼里：她觉得这不可能是偶然。

在相近的时间、相邻的地点，所发生的事情之间一定是有联系的，即我们所常说的因果思维，是多么自然的一种认知方式。动物行为学家们发现[2]，乌鸦中的新喀鸦，就懂得将想要吃的坚果啄抛到十字路口上，在车轮将坚果压坏、绿灯过后，再飞下去捉啄食果仁。这样就既能吃到食物，又能保证自己不被车撞伤。

图1：新喀鸦利用汽车压坏坚果，并趁红灯时啄食果仁

但就是看起来这么简单的事，却代表了某种主体智能水平的核心特质。在图灵奖得主、贝叶斯网络的奠基人朱迪亚·珀尔看来，基于统计相关性的主流机器学习方法，永远无法使机器获得真正的智能。鹦鹉学舌得再精巧，也远比上那只会解决问题的新喀鸦。

至于人类，更是从小就懂因果。除了直接观察现实外，还能通过想象学习：从语言讲述的故事和模型中，就能学到从未见过的新奇知识。甚至习得作为复杂推理载体的语言本身，人类也是小样本学习的典范——完全不需要大量语料，孩子在父母身边随便听听就自然会自己造句了。

没有因果，就找不到规律，无法组织出任何有意义的知识。尽管人类因果思维已经很强了，但似乎仍然有很多现象，隐约有着规律却在知识形式描述之外。它们往往关系错综复杂、变化扑朔迷离，只可意会，不可言传，就如让社会经济学家们和人类个体往往都头疼的社会复杂系统——既然找不到确定的因果，干脆就都当成随机概率和内隐知识好了。

其中最简单是一个两主体交互的例子：爱情——传说中的永恒之谜。爱一个人，究竟是不是让对方爱的原因？无数种知识焦虑被兜售着：“保持高价值”；“真爱，就是付出”；“运气，大样本，试错”……而回到冰冷的现实，又往往是多种情况混杂交织，就如《乱世佳人》中斯嘉丽与白瑞德那纠结的爱情故事一样。

于是很多人放弃了思考，放弃了寻找原因。尽管人类这台天然的因果机器，在直觉上很难相信“去爱”和“相爱”之间没有因果关系（cause and effect）。可如果不再想有努力去做任何改变，任何事就都变成了执念和运气，完全不值得认真对待了。

与之类似的，还有大量对人生具有重要影响的问题：德行与幸福的关系、努力与成功的关系、人际交友的原则、如何进行投资理财……对这些不确然答案的问题，即使你并非口号地“拥抱不确定性”或“适应变化”，往往最终也会随波逐流而泯然于众：要找到一个有确定关系的决策依据实在是太难了。

不过现在情况有所改变，得益于最近几年因果推断方法的研究，人类对因果的理解和形式化处理可能会再上升一个台阶。

从去年到今年，一位新进研究复杂系统、在利物浦大学数学系就读的前哲学博士 Stavros K. Stavroglou，和波士顿大学物理教授 、美国国家科学院院士、金融物理学奠基人之一 Eugene Stanley，共同发表了两篇论文，专门探讨了在复杂系统，尤其是金融市场各种主体要素之间的潜藏的交互作用。他们在传统的因果关系之外，通过加入对对象或事件的时空领域变化考量，定义了一种新型的因果关系：暗因果关系（dark causality），由此发展出一种基于符号动力学和相空间重构结合的因果推断方法，使用包括正、负、暗三种类型的因果模式矩阵表达复杂系统中潜伏和难以捉摸的动态结构，从而得以对所有因果关系类型进行计算、分离和预测。在对生态学、神经科学、金融市场等各种真实系统的广泛测试之后，他们证明这种方法在重构复杂系统隐藏结构之间因果关系的能力上具有相当大的准确度，胜过几乎大多数流行的因果推断方法。

论文题目：

Hidden interactions in financial markets

论文地址：

https://www.pnas.org/content/116/22/10646.short

论文题目：

Unveiling causal interactions in complex systems

论文地址：

https://www.pnas.org/content/117/14/7599

由于其中暗因果关系的定义和发现，具有某种观念革新的意义，为讲清楚，本文先会回顾下因果关系的认知历史和背景 ，然后介绍作者工作，最后对因果关系模型及未来发展进行总结。

一、因果观念的变迁

在神话思维时代，人类对诸如雷电、地震等自然现象都会归结为某个神灵的意志。这种拟人化的目的归因，是人类试图捕捉现象背后本质因果思维的最初尝试，并发展出交感巫术、祈祷等手段与神灵沟通，从而对自然过程进行干预。英国人类学家弗雷泽认为，巫术思维中的“果必同因”的“相似率”，和触染生效的“接触率”，是科学思维的雏形[3]。此时人类已经意识到了世界存在着某种规律，并非万事万物虚幻无常，只能像动物那样被动接受命运。

人类文明的轴心时代，是古希腊人最早发扬了理性精神。哲学和科学的诞生，不仅来自经验知识，更因为是有数学和几何。古希腊最早的哲学家，包括泰勒斯、毕达哥拉斯等，都同时也是数学家和自然科学家。数学对象之间的必然关系，放到经验世界，就产生了让哲学脱胎于神话的第一次天问：“世界如何起源的？从此人类以理性思维探讨世界秩序成为了可能。

希腊哲学家对世界起源的回答，无论是水、数、活火与逻各斯、气或无定形，最后都被亚里士多德总结为四种原因（cause）：质料因（hyle）、形式因（eidos）、动力因（kinesis）和目的因（telos）。

图2：亚里士多德四因说：一个桌子得到形成

在四因中，涉及物理世界的是前三种，大体对应物理意义上的物质、信息、能量。其中形式因最重要，它不仅适用抽象理念还关乎具体事物，决定了一个事物与他者根本不同，并且往往可以囊括另外三者。亚里士多德本人持有一种形质论（Hylomorphism），认为形式和质料结合决定了某个事物一切。此外他还首创了目的因，这意味着在原因中可能存在某种主体意向性。

目的因在某种意义上继承了神话思维，是一种“解释”（reason）——可见这时哲学家们还没有区分出解释与 “原因”（cause）的不同，也没有充分因（sufficient）和必要因（necessary）的概念。

到了17世纪，另一位百科全书式的学者——德国数学家和哲学家莱布尼茨，提出了“充足理由律”（Principle of sufficient reason）：“任何事物都有其存在的充足理由”，甚至将其列在逻辑学三大定律（同一、矛盾、排中）之上。充足理由律确信所有事物都有其是如此而非其它的原因，只不过人们未必能找得到。莱布尼茨在最高逻辑层次肯定了充分因，使它成为一切科学和理性活动的基础。此外，莱布尼茨还有一个我们世界是所有“可能世界”最好的乐观信念。

18 世纪重要的哲学家休谟则先后在《人性论》和《人类理智研究》中给出了因果关系两个定义：第一个诉诸“两个类似的对象在时间上先行和空间上的邻近的关系”，第二个则表达为“假如没有前一个对象，那么后一个对象就不可能存在”。第一个定义将因果关系表达为观念间的联结，第二个则涉及到了反事实推理的必要因，也即“若非因”（but for，之前莱布尼茨论证可能世界时已用到必要因推理）。但不管哪一个，休谟都已经将因果关系限定在了客观经验世界的具体对象中。在休谟看来，理性能研究的两类对象，纯粹观念的关系（Relations of Ideas），如数学和几何是确定的，然而建立在因果观念上的实际的事情（Matters of Fact），却是不可靠的，只不过是人类因为记忆和经验习惯“恒常连接”的产物。

充分因：A → B，有之必然，无之未必不然。“投资”是“移民”的充分因，但也通过“结婚”；

必要因：¬B→¬A，“没它不行，有它不够”。若不是英国国籍，就不能竞选首相。英国籍是竞选首相的必要因。可见，找到必要因必须涉及反事实推理。

19 世纪德国哲学家、唯意志论创始人叔本华，在博士论文《充足理由律的四重根》中给出了莱布尼茨的充足理由律的四种表现形式：

1. 因果关系（Becoming）：生成/变化的充足理由律，适用于现实对象；

2. 逻辑推论（Knowing）：认识的充足理由律，适用于逻辑对象；

3. 数学证明（Being）：存在的充足理由律，解释时间和空间的必然性；

4. 行为动机（Willing）：行动的充足理由律，解释动机和行为之间的必然性。

在此叔本华已经明确区分出，科学最为关注的因果关系是充足理由律在现实对象中的体现。此外它还体现在逻辑、数学和意向系统不同领域的关系中。后面我们会看到，另外三重根对因果观念复兴和发展起到了关键作用。

尽管如此，对现实对象和事件之间因果关系的本性，是主观还是客观，是不确定性还是确定，不同的信念和假设，依然经历了一个跌宕起伏、针锋相对且漫长的过程，而这都与科学的发展状况有关。

回到 17 世纪，牛顿创立经典力学之后，一时决定论占据了所有学科领域的核心：包含世界在内的整个时空都看成了一系列确定性因果事件的链条。法国数学物理学家拉普拉斯的一句话最为著名：“只要给我足够的初始条件，宇宙所有粒子初始位置和速度，我就可以预测一切”。

但随后，本意是想效法牛顿在精神道德和政治领域建立一个科学的体系的休谟，却开始怀疑因果关系的客观有效性，就像那只随时可能被杀掉的“罗素的火鸡”一样：从“实然”（本来是）并不能推出“应然”（应该是）。此外，还有同一时代的牧师兼数学家贝叶斯，也将概率现象解释为主观信念程度的变化和更新，让概率本身也失去了客观性。

然而“除了物理学之外，都是集邮”（卢瑟福），纷纷效法物理学的其他自然和社会科学并没有取得想象中确定性的成功。到了19 世纪，统计学创始人高尔顿、以及他的学生作为统计学之父的卡尔·皮尔逊，则干脆用相关关系（Correlation）取代了因果关系，认为因果关系只是相关关系的一个特例。

进入 20 世纪，就连在物理学中人们也发现了更多不确定性现象。量子力学对微观世界的描述，让很多人确信，世界在根基上就是不确定性的。混沌理论革命则让人们意识到，对复杂系统即使存在确定的关系，也会因为初始敏感导致计算不可约性。

在这些科学发展的背景下，不确定性完全占据了上风，大多数人认为可能只存在相关性，在科学实践和决策上也广泛采取统计学方法。科学反映客观实在的观念已一去不复返，物理定律也降格为基于某种观测数据拟合的理论模型。

科学家对统计方法如此依赖，以至于在现代计量经济学家格兰杰（Clive Granger）在给出近代第一个有关因果关系的形式定义时，也是以概率形式给出的。如今倡导因果关系革命的朱迪亚·珀尔，在早年也曾全心拥抱统计学方法并创立出对人工智能有重要影响的贝叶斯网络。

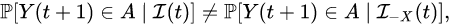
方法图：Granger 因果检验，若X存在与否让下一时刻Y出现概率发生了变化，则X是Y的一个格兰杰因

然而珀尔在随后的研究中发现，统计相关性并不能取代因果性，它无法处理具有共同混杂因子的变量关系，就像鹳鸟并不导致婴儿出生一样，统计数据常常倒因为果，或造就伪相关。过于依赖于数据和算力的人工智能，不仅要求数据独立同分布，泛化能力很差，其对抗脆弱性（adversarial vulnerability）更使得在意外场景中即使微小干扰也会造成严重误判。简而言之，没有因果模型，纵万千数据，也是鹦鹉学舌，比不上一只能吃到自己坚果的乌鸦。

珀尔认为，现在人工智能只处于“因果关系之梯”的第一阶段：观察，其本质是关联，被动发现数据中的规律。另外两个层级是干预和反事实推理（想象），分别是主体介入后预测行动改变环境的能力，以及在虚拟世界获反思和理解事件因果关系能力。

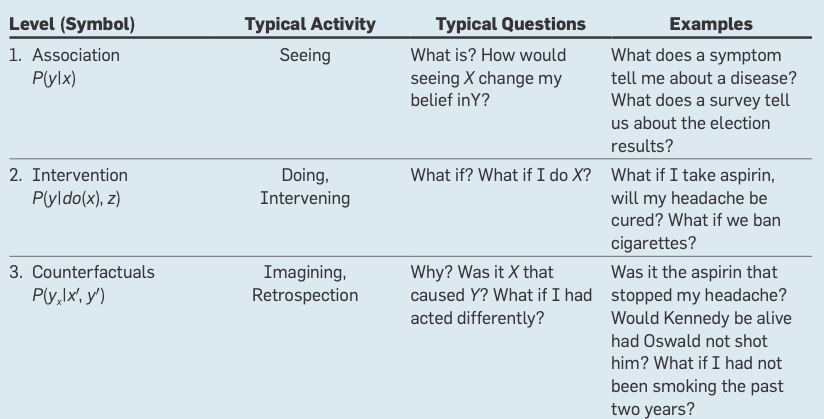
图3：因果关系之梯，关联、干预、反事实想象。注意这里采取概率或函数表示都无关紧要。例如在第二层， do 算的“干预”结果，与格兰杰因果基于观察的数据定义是不同的。前者会主动增加鹳鸟数量，再去计算婴儿数量，发现二者并无因果关系

虽然珀尔本人并不关心因果实在与否，只是从技术实践角度对因果进行研究。但他的因果思想，尤其反事实定义，确实来自逻辑学对因果语义的研究，由美国哲学家学家大卫·刘易斯提出的模态实在论（modal realism），认为在探讨必要因（休谟有关因果第二种定义）时，“若非…”中那个与我们最接近的可能世界都是真实的。有了可能世界的情景，我们才能反对什么是必要的。

例子：“法院命令 → 队长传令 → 士兵 A 开枪 → 犯人死亡”。

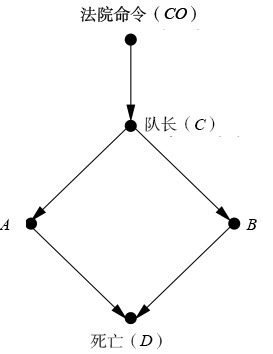
图4：因果图：A 是 D 的充分因，但不是必要因。因为若非 A 开枪，B 也会遵循命令开枪

显然，必要因处理反事实事件，能有效定位和处理特定具体事件的原因和责任。我们看到，在因果推断从统计方法中复苏的过程中，哲学思想起到了关键的作用。

更一般的，通过将宏观物理的确定性模型（机械/物理模型 Mechanistic/Physical）的特定解作为条件，对必要因和充分因进行形式化，我们可以得到因果图和结构因果模型（SCM,Structural Causal Model），从而将反事实视为状态函数在因变量取某个值的一个潜在结果。这与诸如牛顿力学中那样传统物理模型，单纯表达宏观充分因素之间的的影响是不同的。

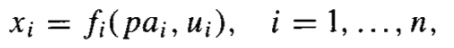
（一个一般的结构因果模型[4]：在状态函数 f 中 pa 是影响 x 的父变量因素，u 是忽略干预的默认状态。当仅考虑线性因素时就是结构方程模型（Structural Equation Modeling,SEM），引入特定解作为条件就变成了结构因果模型，后者与因果图的区别在于，状态函数 f 的变化可以是连续和非线性的）

例如，令变量 X 的值 xi 为志贵在时间 i 的健康状态，A，B 是影响 x 的干预因素，U 是不采取任何行动的默认状态。令 A =  “服用芬太尼”，B = “早起床”，于是志贵的健康与 A、B 的结构因果方程为：

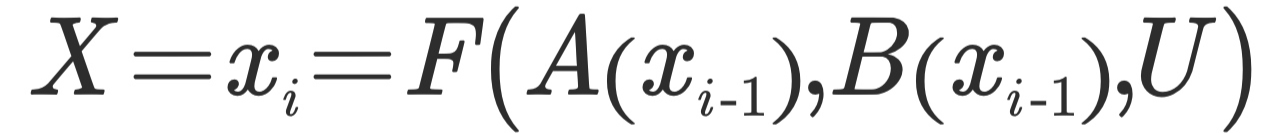
这时，可以很容易表达在某个特定事实时 X 的状态值，例如 F(A=0,B,U) 代表不服用芬太尼时志贵的状态——如果志贵变得更健康了，那么通过反事实推理，就说明变得健康与服药没有关系。我们可以看到，不同时间状态之间，干预变量之间可以存在相互作用，可以是连续、离散，线性或非线性的。

尽管如此，从方程中也能看出结构因果模型一定局限，尽管它可以表达连续状态，但与因果图一样它最善于处理还是单独时间点上离散的事件性因果（Event Causation）。例如 “上一天不健康，服药，晚起” → “第二天健康，默认不干预”。

显然，这些某些条件下具体事件的关系，很难上升到更普遍因素如（“吃药”和“早起”）之间的因果关系。如果要这么做的话，就意味着要去不断随着时间循环处理一次又一次具体事件——于是就变成了诸如类似存在持续交互作用的情景。例如，人类个体之间的恋爱关系、捕食者和猎物之间的关系，以及金融市场中的交互反馈等中，这些要素之间互相反馈互为因果——属于一种过程性因果（Causal Process)。如果说事件性因果是单向链条的话，那么过程性因果就是一条绳子，变量之间会因为拉扯导致方向大小随时改变[5]。

因此对这类关系，即使X和Y之间可以表达为某种函数关系，如果采用结构因果模型去分析，就会出现因果环路打破了有向无环图结构。这种循环因果结构，很难分离和处理，其中因果环路图（Causal Loop Diagram）[6]是一种初步的分析方法，但目前还没有通用基于数据的方法去有效识别和计算。

那么，如何解决这种因果关系呢？就如十万年前丹尼索瓦人小女孩和休谟的因果定义所启示一样，我们可以不仅考量变量本身，更进一步去考虑变量最近时空邻域（Nearest Neighbors）的变化模式，例如志贵健康程度在一定时间范围内的变化模式，与服药剂量在相应时间内的变化模式是否一致（甚至包括志贵所在的环境，与药品环境），如果遵循相同的模式，那么就可以认为它们之间具有正向或反向的因果关系。如果不一致，但是有稳定的不一致，那么就认为它们之间存在一种可识别的非线性因果结构——即暗因果关系。

下面我们会看到，两位作者所发展出的基于符号动力学的最近邻相空间重构方法，就为研究变量时空领域之间的因果变化模式，即非线性——暗因果关系提供了一个有效的解决方案。但在此之前我们先要知道什么是暗因果以及它们是如何表示的。

二、暗因果关系的发现

暗因果并不神秘。虽然识别暗因果关系最有效的地方在于对数据建模，但在最简单的动力学方程中就有非线性因果存在（也因此两位作者在论文附录中饶有兴趣地测试了很多理论模型）。

让我们回到最开始最简单也最难解的恋爱的例子：恋爱中明明只有两个人，为什么关系发展过程却往往扑朔迷离、充满不确定性？为什么即使一方对另一方好，甚至双方都着为彼此着想，两人的关系也可能不像期望那样完美的方向发展？

美国著名的数学与非线性系统专家、小世界网络模型的提出者  Steven H. Strogatz 曾经提出一个恋爱动力学模型[7]，从两个变量就刻画出了恋爱关系变化的复杂模式。

罗密欧爱上了朱丽叶，但在这个故事版本中，朱丽叶是个充满不安全感、不稳定的恋人（即依恋关系中的恐惧型依恋 [8]）：罗密欧越爱她，朱丽叶越想逃离并躲起来。但当罗密欧心灰意冷后退时，朱丽叶又发觉出他的好，舍不得离开而转身回来；另一方面，罗密欧也会倾向正面回应她的情感：当朱丽叶爱他时，他会活跃起来重新爱她；但当她疏远他时，他也会变得冷淡。我们用 R 和 J 两个变量分别代表罗密欧和朱丽叶的感情：

R(t) = 在时刻 t，罗密欧对朱丽叶的爱/恨

J(t) = 在时刻 t，朱丽叶对罗密欧的爱/恨

于是，他们充满纠结的的恋爱方程模型为：

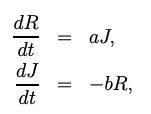
显然，这是一对互为因果的变量，属于过程性因果，二者之间作用是一种非线性因果关系。

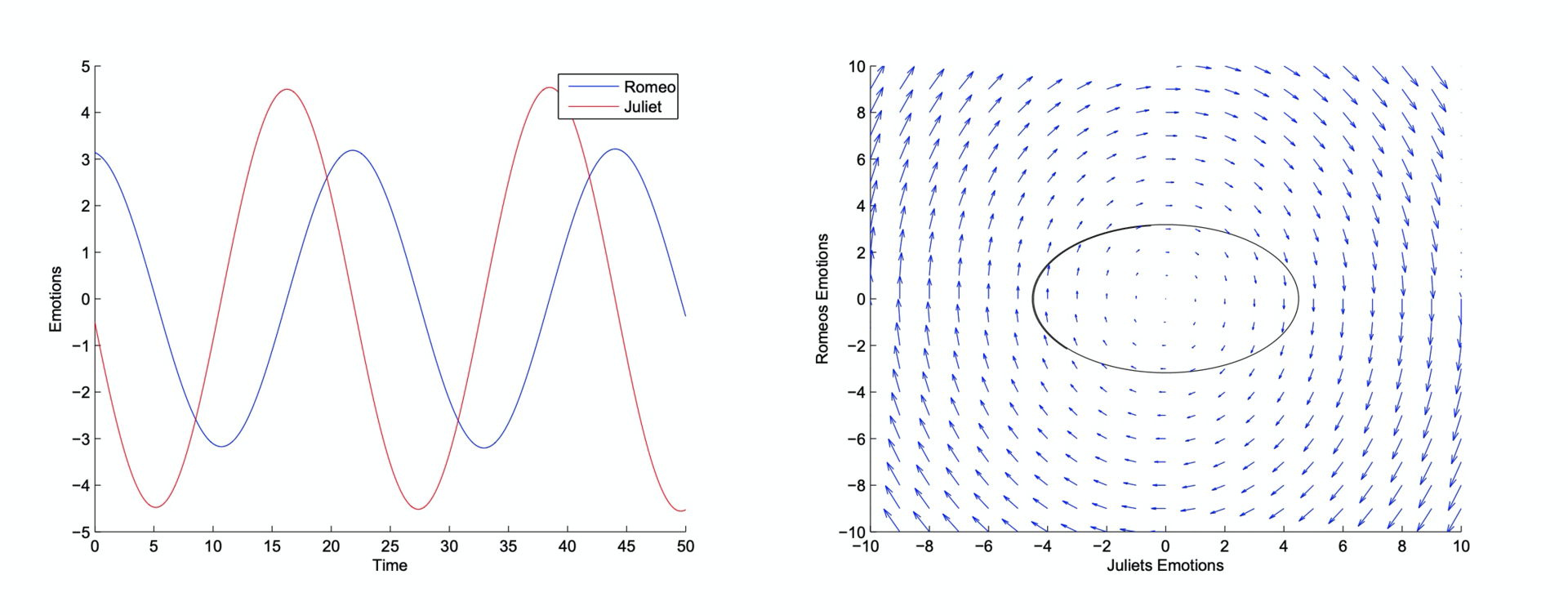
图5：罗密欧与朱丽叶的恋爱动力学曲线

在上图，我们可以看出，罗密欧和朱丽叶之间的爱情将是永无止境的“热情-冷漠”循环。如果以事件性因果来看，R 和 J 之间并没有明确的因果关系：当罗密欧的 R 增加时，朱丽叶的 J 在不同时间可能会降低、也可能增加，反之亦然。

但二者变化又不是随机的，或者相关关系，如果直接计算变量会发现他们的相关系数是变化的。

如果我们以 τ 表示变量变化的时间延迟间隔，以符号⬈、➡、⬊ 表示变量增减情况的话，即：

⬈：X(τ) < X(t+τ)，即 X 值增大

➡：X(t) = X(t+τ)，X 值不变

⬊：X(t) > X(t+τ)，X 值减少

会发现 R 和 J 之间遵循以下变化模式：

J⬊ → R⬊ → J⬈ → R⬈ → J⬊……

J⬊ → R⬊ → J⬈ → R⬈ →这种作用模式，在整体上形成一种平衡反馈回路。如果单从两个点取值之间的事件来看，完全看不出哪一种关系占据主导。那么如果不仅考虑点、而是包括包裹点的邻域点集的变化情况呢？J⬊……

让我们回忆下休谟有关因果关系的第一个定义：

……它是先行于、接近于另一个对象的一个对象，而且在这里，凡与前一个对象类似的一切对象都和与后一个对象类似的那些对象处在类似的先行关系和接近关系中……

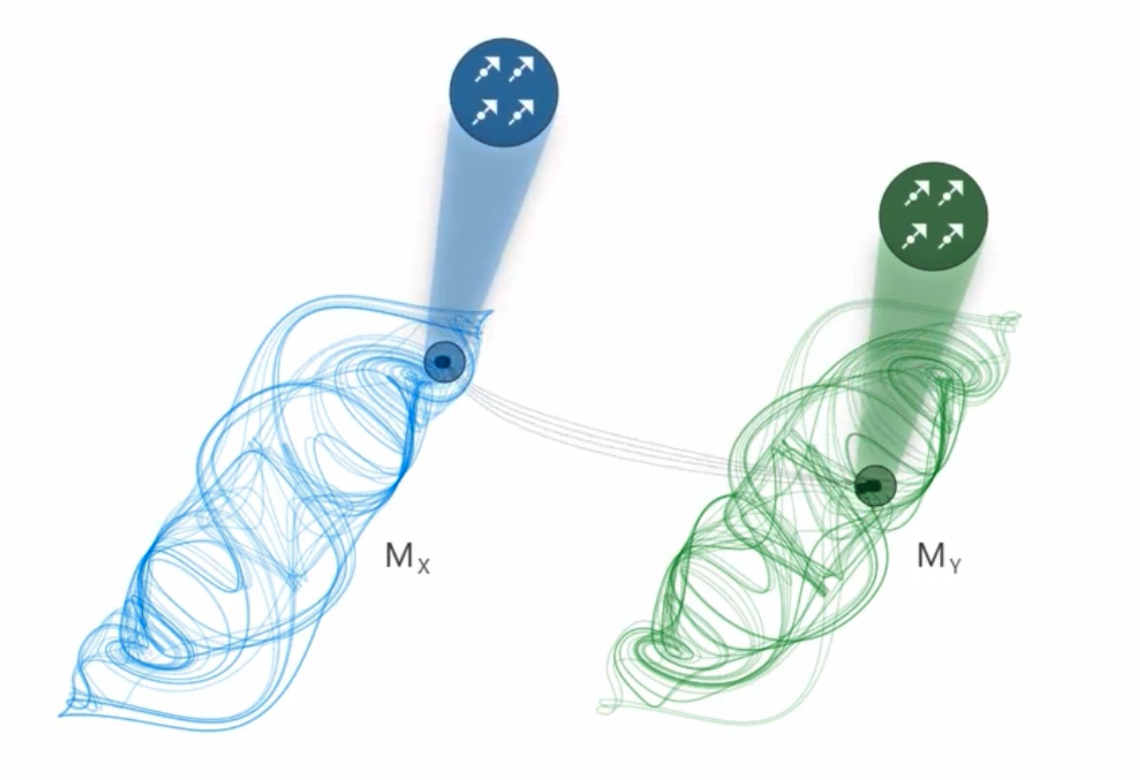
图6：从点到邻域点集：不仅要考虑点本身，还要考虑邻域点集的变化模式

在休谟看来，因果关系本来就是由于空间上的邻近和时间上的先行、类似对象之间的关系导致观念上的联结——换句话说。如果仅仅是考虑对象本身，不考虑对象周围的时空邻域，就更难找到（形成）真正的因果关系（观念）。正如开始的干雷暴导致森林大火，那样判断一定是干燥高温下，如果是空气湿度较大雷雨的话，那么雷电作就很可能不是原因了。

当然，更重要在数学上，对于以微分方程形式呈现的动力学方程而言，柯西-利普希茨定理（Cauchy-Lipschitz Theorem）[9]决定了f 存在局部解乃至唯一的最大解，使得在局部范围内 X(t+dt) 可以完全由 τ 时间之前的 X(t)决定。这就说明，对非线性变化，是可以提取出直观而准确的某种因果模式的。

因此，如果我们也考虑变量邻域变化的话，会发现罗密欧与朱丽叶情感遵循以下模式：

J⬊⬊ → R⬊⬊

R⬊⬊ → J⬊⬈

J⬊⬈ →  R⬈⬈

R⬈⬈ → J⬈⬊

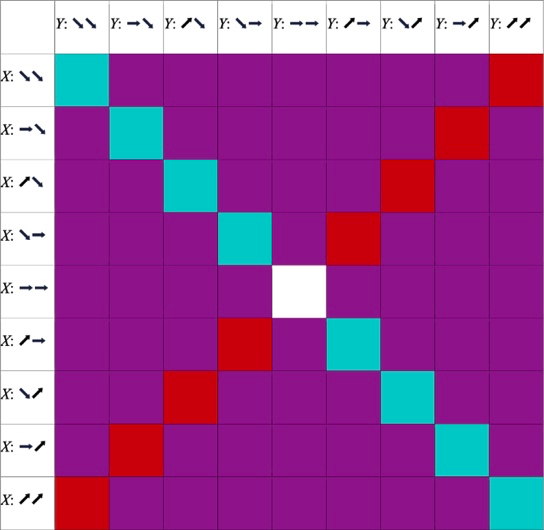
现在我们已经可以分离因果模式了：可以看到，除了第一个关系外，其他三个关系都不是传统因果关系模式。两位作者认为，这种在邻域内非正向或负向反馈的关系，可以定义为一种新型的因果关系，即暗因果关系。我们可以通过对任意维空间两个或多个变量邻域点集变化情况进行总结，分离出所有因果作用模式，分别计算其权重，写在下述因果模式矩阵（Pattern Causality）中，并提出三种因果关系的强弱函数，最后判断究竟是哪一种因果模式占据主导。

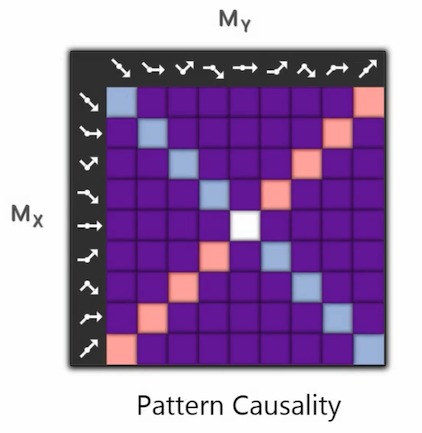
图7：因果模式矩阵：蓝色代表正因果，橙色代表负因果，紫色代表暗因果

这里可以稍微解释下这个方法的效果：例如，前面四个变化模式中，可以看到有三个关系都是暗因果关系，占 75%。但即使如此，我们依然提取出了一个确定因果关系：J⬊⬊ → R⬊⬊，翻译过来就是冷漠导致冷漠。这给我们的教训是，不仅恋爱甚至无论什么关系，疏离总会导致疏离。除此之外，暗因果也不是运气或随机，是真实存在的作用模式，也许我们很难把握，但要相信它的存在，把握住我们能把握的部分就好。

暗因果关系本质是从变量的非线性作用分离出邻域变化因果关系的模式，它既非相关，又非通常意义上的单向因果，可以认为是过程性因果的肖像，就像对因果绳子形态进行了素描。例如，在状态空间维度 E=4，对 X→Y关系中，有一种最典型的暗因果作用模式：

Px = ⬈⬈⬈⬈  → Py = ⬊⬈⬊⬈，代表 X 持续增强引起 Y 的振荡。这种暗因果关系在现实中也存在，比如心理过程中父母对子女的持续的溺爱。

不仅在理论模型，在诸如在生态系统、大脑神经系统和金融市场中都存在大量的暗因果关系。有了这种符号动力学分析方法后，我们就可以计算出一个系统中究竟哪一种因果模式占据主导地位，从而对系统有更好的理解、做出更好的预测。

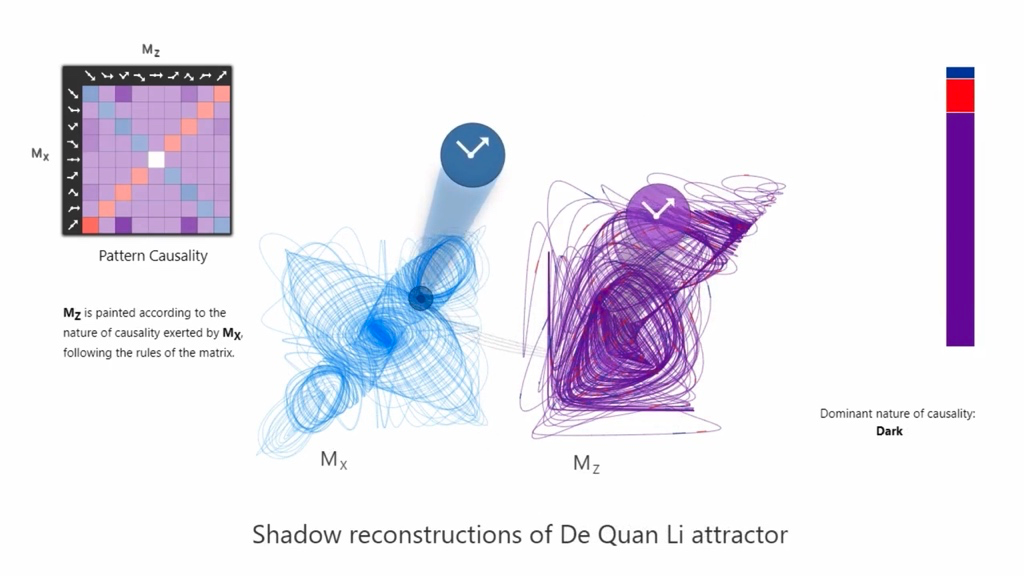
图8：在 Dequan Li 吸引子中，暗因果关系比例是最高的

三、计算时空邻域与因果模式矩阵

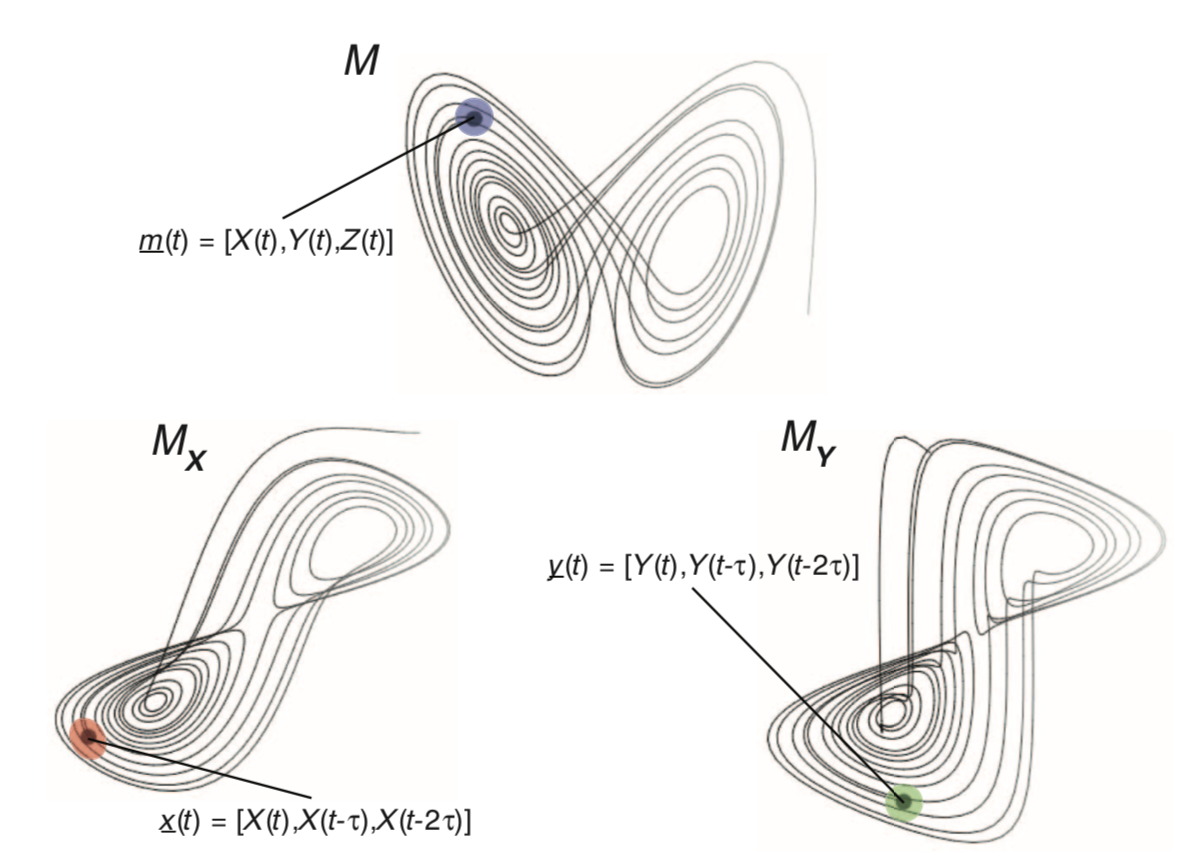
二位作者在引入符号动力学方法后，基于传统的相空间重构发展出一套分离和计算复杂系统不同因果模式的方法。

如下图所示， Mx 和 My 都是动力系统 M 重建的吸引子（通过投影到某一维度坐标重建，所以也被称为影吸引子），因此理论上必然具备因果关系。然而如果单纯考虑变量 x(t)和 y(t)本身的变化的话，如上一节所述，会发现二者没有稳定的因果关系。因此作者分别计算出两个吸引子邻域 NNxt 和 NNyt（以及预测 Mx的 ） 的因果模式，分离出三种因果关系，并比较它们的不同，最后确定影响最大的因果模式类型。

下面会讲述作者的计算方法，内容会有一定技术性，建议非专业读者可以暂时跳过。在看之前，大家可以看下官方对方法讲解的视频。

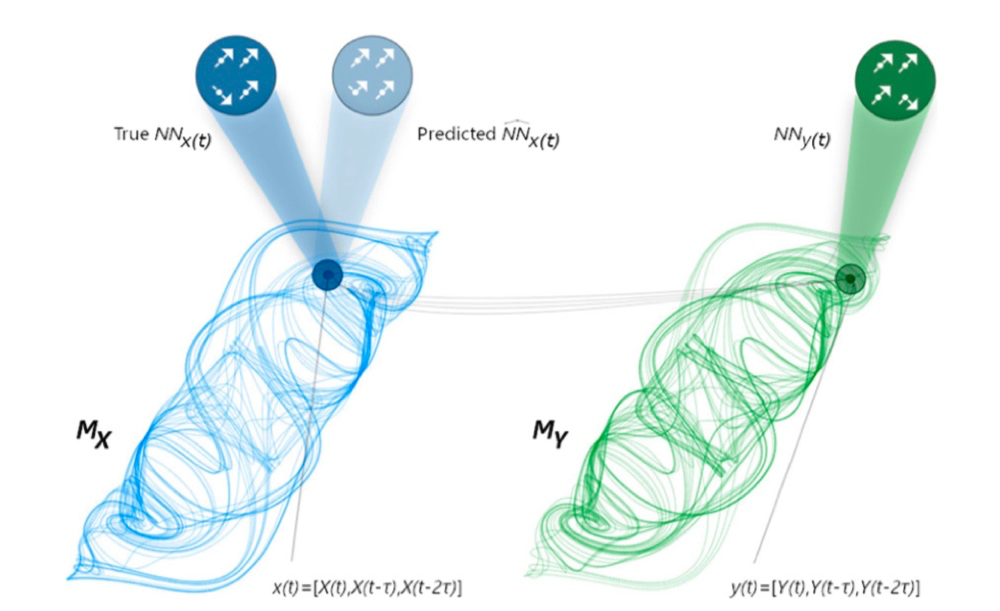
图9：基于最近邻域符号动力学的吸引子重构

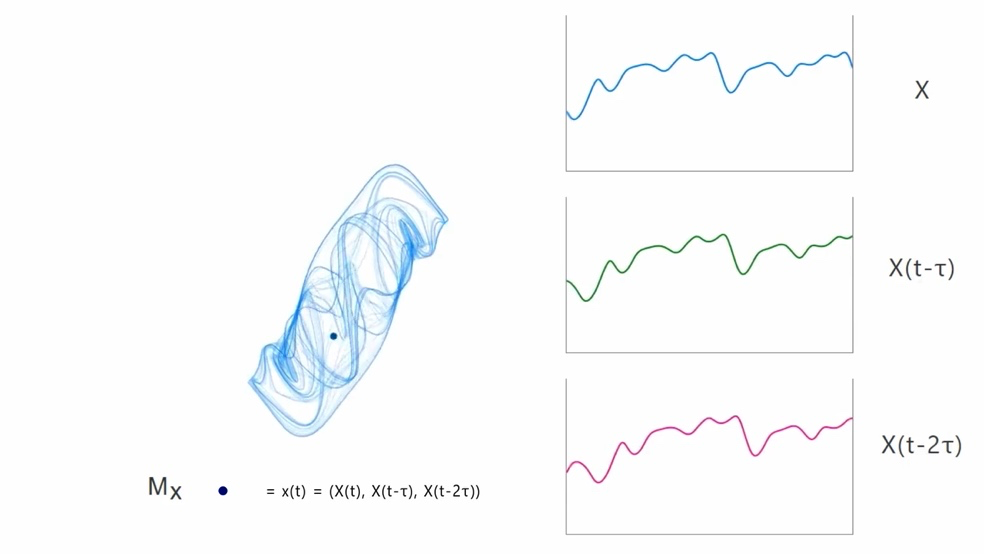
1. 影吸引子重构：X(t),τ,E → Mx

对于任一在 m 维状态空间 R^m 上演化的动力系统 M，已知映射到笛卡尔坐标下的离散实值时间序列函数 X(t)∈R，令 X = {X(1),……, X(L)} ， L 为时间序列的长度。我们的目标是从 X(t) 重建 M 的影吸引子Mx。

根据 Taken 定理（Taken theorem）[10]，通过选取合适的嵌入维 E 和 延迟 τ，可以从 X(t）的延迟序列对原始相空间进行重构：

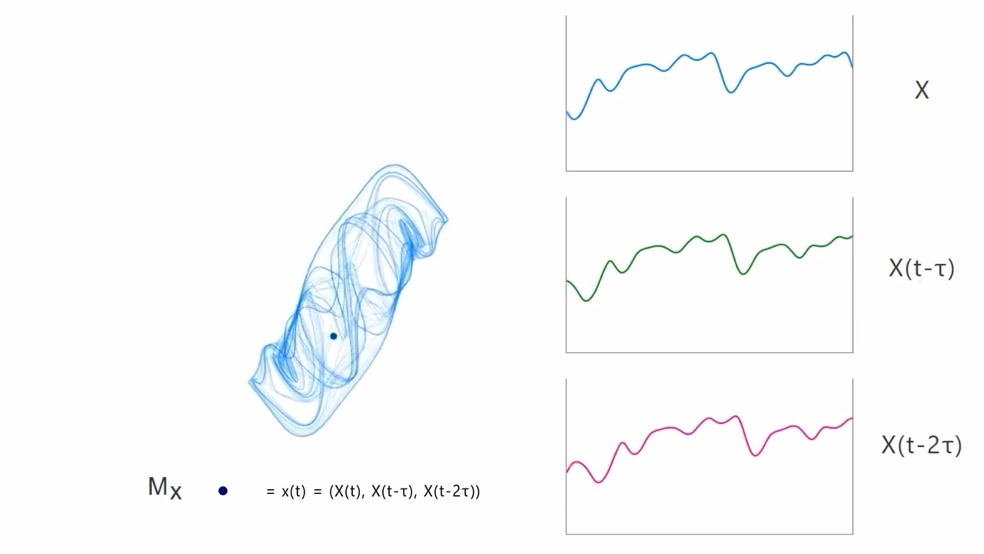
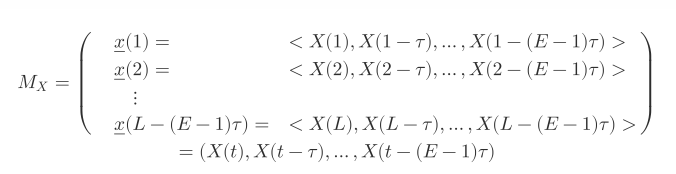
可见 Mx 是 E*L 矩阵（注：Mx 中<>表示序列值为矢量，且为了便于观看理解针对原论文调整了顺序），当 E = 3 时，

 

 

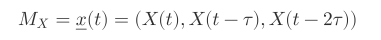
对已知 M 在 y 轴投影的时间序列 Y 同理，同样可以重建影吸引子 My。

2. 计算吸引子距离矩阵：Mx,L → Dx

在计算 Mx 的时空邻域之前，我们必须确定一种对吸引子空间合适的度量，并计算 Mx 的距离矩阵 Dx ∈ R^(E-1)。通常可以考虑两种度量，分别是曼哈顿距离（Manhattan distance），和欧几里得距离（Euclidean Distance）。如果要平等对待所有节点，一般使用前者，相反如果要降低更大距离的权重，则使用后者。二者分别记为记为L1、L2，则根据定义有：

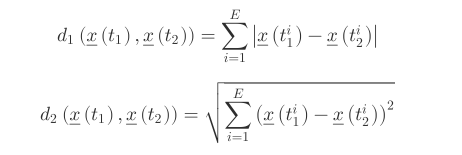
欧几里得距离即平面距离在高维的推广，与曼哈顿距离区别直观表示如下。可以看到，代表红黄蓝色的曼哈顿距离均为 12，而绿色的欧几里得距离有6×√2 ≈ 8.48。

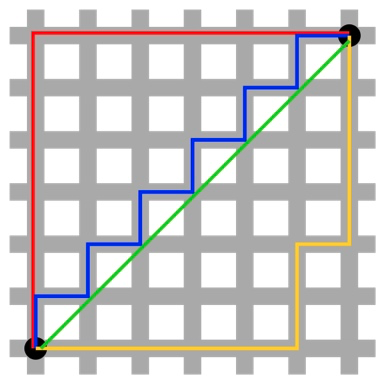
图10：欧几里得距离（绿）和曼哈顿距离（红黄蓝）

故而 Mx 的距离矩阵 Dx 为：

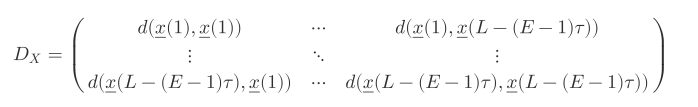
同理可以计算出 Dy。

3. 计算吸引子最近邻域：Mx,Dx → NNx

有了 Dx ，对 Mx 上 每一个点 x(t)，我们都可以计算出它的最近邻域 NNx(t)

由于 Mx∈R^E，故对其中每个点，都有 E+1 个最近邻。例如当 E=3 时，x(t) 会有四个最近邻在NNx(t) 中。

在这里，我们可以看下最近邻域对应的几何意义，它就是数学上的有界单纯形（bounded simplex）。n-单纯形是和三角形类似的n维几何体，定义为n维以上的欧几里得空间中的（n+1）个仿射无关点闭包集合，其中 1、2、3 单纯形分别为线段、三角形、四面体……等，如下图所示：

图11：最近邻，在1~20维空间的几何意义有界单纯形

于是可以直观看到，对点 x(t1)∈Mx，当 E=3，会有四个最近邻域点，记：NN x(t1) = {s1,s2,s3,s4}

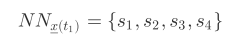
注意，不同于影吸引子空间，对每个 x(t)∈Mx，对应的最近邻 NN x(t) 时间索引下标都是从当前时间点 tx1 而非从 t=1 开始的。

因此，时间序列点为 tx1、tx2、……、txE+1 的 E+1 个最近邻为：

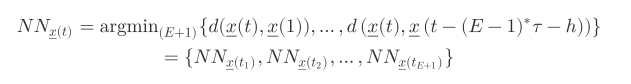
注意上面，之所以求到 d(x(t)，x(t-(E-1)*τ-h），即少h 个时间点，求而非求 x(t)和所点距离最小的 E+1 个点，是为了多出额外h 时的数据点，通过 Mx 对 My 进行预测（即 计算 Mx 预测 h 时间后情况，与My 的最近邻情况对比）   

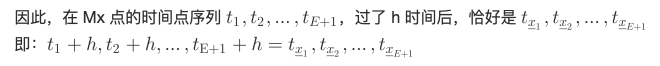
故可以计算出对应 My 的时间序列点最近邻距离为：

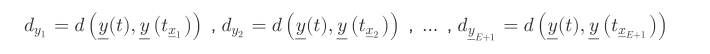
到这里，我们可以看到与传统相空间重构方法如收敛交叉映射[11]（CCM，Convergent Cross Mapping）的差异。

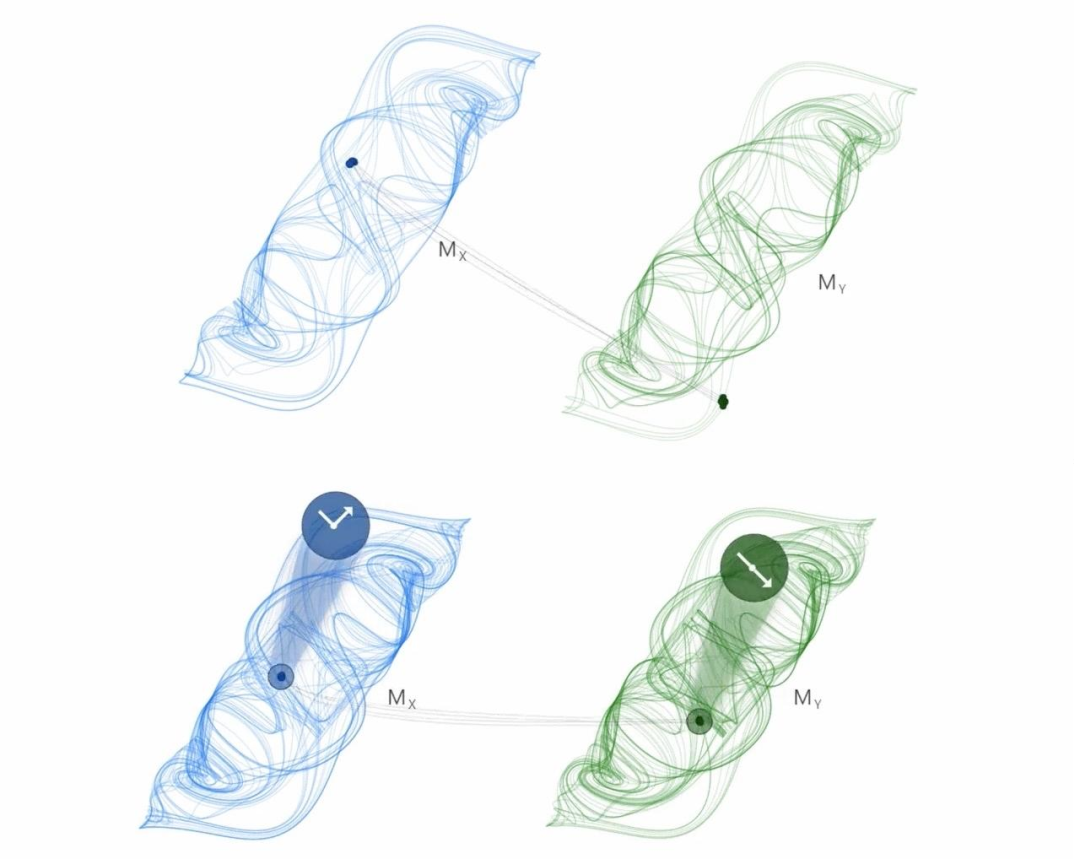
4. 计算最近邻的因果模式：NNx →Sx→Px

因为Mx，My 是已知的，我们可以计算出它们所有点的最近邻序列。同理，可以计算出在 h 时间后，通过 Mx 对 My 预测的最近邻序列。然后我们通过对比实际 My 的最近邻因果模式和预测的因果模式，就可以知道在 h 时变化中，Mx 对 My 究竟有多少是正向因果作用、负向因果作用或不明确的暗因果作用。

通过前面计算，我们已经知道，对于点 x(t)、y(t) 都对应有E+1 个点的最近邻。例如当 E=3 时，对点 y(t1)∈My，每个邻域会有四个最近邻域点，记为

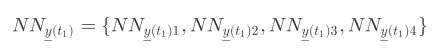
每个点都是三维时间序列的点，如NNy(t1)1 = {0.13,1.25,3.26}。并且有相应时间延迟的变化以及因果变化模式。

对于：

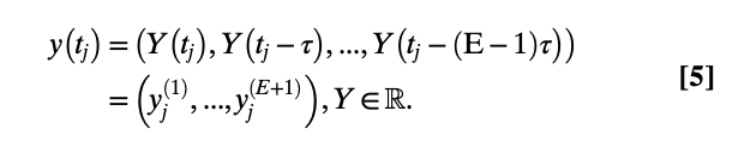
我们可求得所有的变化模式 s：

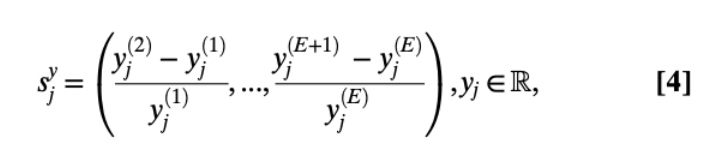
例如，E=3 有四个点的变化模式，我们可以求得：

S= {s1,s2,s3,s4} = {(0.32,0.45),(-0.11,0.51),(0.13,0.19),(0.05, -0.08)}

然后根据以下符号规则（以 X 表示，换成 Y 或其他变量同理）分别计算出它们在时间延迟 2τ 和 τ 的变化量以及相应的模式。

⬈⬈：X(t-2τ) < X(t-τ) < X(t)

➡⬈：X(t-2τ) = X(t-τ) < X(t)

⬊⬈：X(t-2τ) > X(t-τ) < X(t)

⬈➡：X(t-2τ) < X(t-τ) = X(t)

➡➡:  X(t-2τ) = X(t-τ) = X(t)

⬊➡：X(t-2τ) > X(t-τ) = X(t)

⬈⬊：X(t-2τ) < X(t-τ) > X(t)

➡⬊：X(t-2τ) = X(t-τ) > X(t)

⬊⬊：X(t-2τ) > X(t-τ) < X(t)

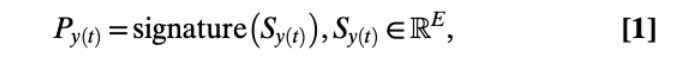
因此，s1，s2，s3，s4 因果模式签名分别为：

P(s1) =（0.32,0.45） = ⬈⬈

P(s2) =（-0.11,0.51）= ⬊⬈

P(s3) =（0.13,0.19）  = ⬈⬈

P(s4) =（0.05, -0.08）= ⬊⬈

那么影吸引子在最近邻域的变化模式和因果签名究竟是被哪个邻域点决定呢？这就需要对最近邻上所有点进行加权求平均。

而对最近邻因果模式求平均的权重，是通过之前定义的度量 Dx 获得的，可以由以下公式3进行计算（这里采取的是曼哈顿距离），然后通过公式2计算出最近邻变化的评价值。

例如，对于上面的 s1，s2，s3，s4，分别带着权重 0.91，0.54，0.82，0.69 我们可以求出评价的 S：

S = 0.91 (032,0.45) + 0.54 (-0.110.51) + 0.82 (0.13,0.19) + 0.69 (0.05, -0.08)  =（0.3729,0.7855）

即 S 的加权平均后的因果签名是  P = Signature(S) = ⬈⬈

图12：最近邻域的平均模式签名

因此，如果我们得到在 My 上某个点邻域的因果签名 Py = ⬈⬈，而在 Mx 上相应点因果签名为 Px = ⬈⬈。由  Px = ⬈⬈ →  Py = ⬈⬈，我们就说 Mx 上的点 x(t) 和 My 上的点 y(t) 具备了正向因果关系。

因为Mx，My 是已知的，我们可以计算出 Mx 所有点的最近邻序列变化以及因果模式签名。以及计算出在 h 时间后，My 实际上的和通过 Mx 对 My 预测的最近邻序列的变化和因果模型签名。三者分别用以下表示：

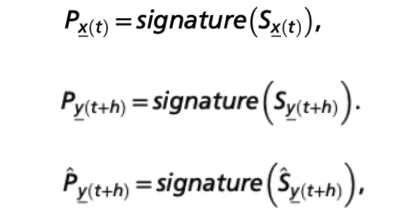
5. 填充因果模式矩阵：Sy,Sx → PC

我们可以将所求得在 h 时间后后 My 的平均变化值，与 Mx 的相应领域的平均变化值，分别求范数，并求比值：

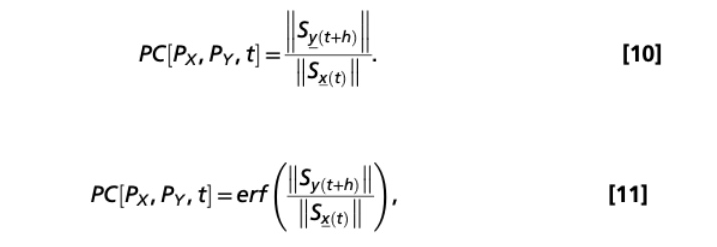
在通过 11 即高斯误差函数归一化输出后，从而得到 Mx 到 My 的一个因果模式矩阵。

6. 分离因果关系影响函数：PC → Pt,Nt,Dt

对因果模式矩阵分块进行计算，可以得到分别代表三种因果类型影响的（正、负、暗）函数 P(t)、N(t)、D(t)：

最后就可以使用诸如最小/最大生成树 [12,13] [14] 之类的算法对网络进行过滤，以仅保留最强的关系。

四、应用例子与效果对比

生态系统的例子

首先以理论生态模型：共生、竞争、替罪羊的例子作为方法效果评估对比。

A：互惠共生（Mutualism），两个物种 X，Y，如鳄鱼与牙签鸟之间的关系；

B：种间竞争（Interspecies competition），如羊和兔子之间是竞争关系；

C：替罪羊（Scapegoat），两个物种 X，Y在捕食者 Z 下的种间竞争，如牛、羊在狮子之间的关系。

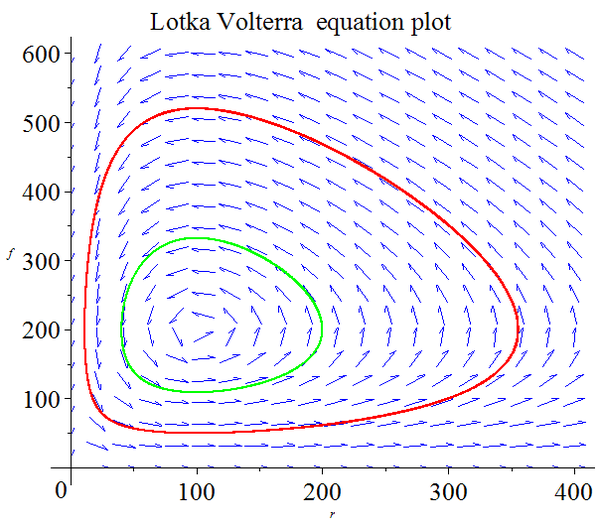
对生态种群数量之间的变化描述通用用 Lotka–Volterra 方程描述：（y 是捕食者的数量，x 是猎物的数量）：

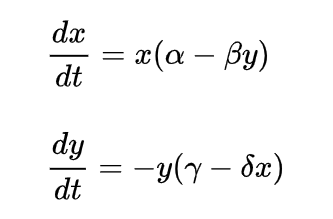
其相位变化通常为：

至 C 的情况则是一个 1 捕食者-2 猎物（one predator–two preys）需要三物种 Lotka–Volterra 方程描述 [14]。

下面三张图表示了三种关系的随着时间种群人口数量变动情况。

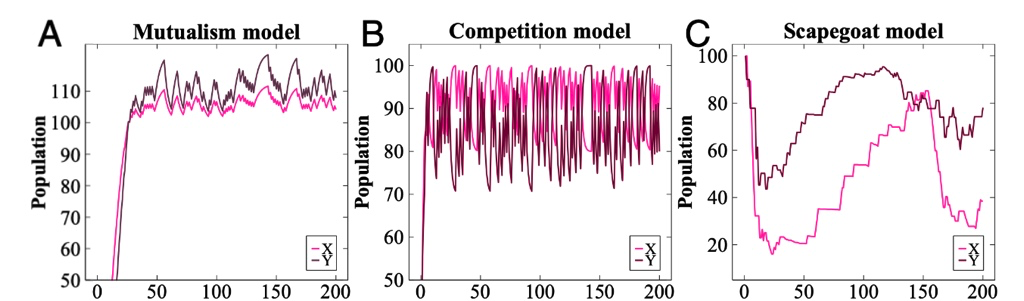
图13：共生、竞争、替罪羊的种群人口变动情况

因为变量之间存在着非线性作用，用传统方法很难分清 X 和 Y 之间究竟存在什么关系。例如，通过相关性分析，会得到以下结果：

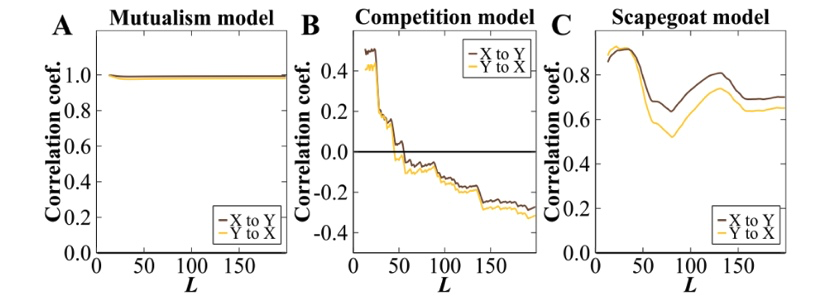
图14：共生、竞争、替罪羊的相关系数

由皮尔逊相关系数定义可知，X、Y 之间的关系是对称的，

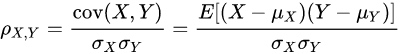
然而在上图中可以看到，除了共生模型中二者因为种群数量几乎同步涨落而稳定外，X 和 Y 之间的关系都已开始撕裂脱离。这意味着在非线性系统变量作用中，二者之间并不是相关关系。

如果以 β 系数（Beta coefficient，一种判断股票或证券价格相对市场整体波动性的方法），对于除了对共生模型在一定时间后稳定有相对稳定的结果外，竞争和替罪羊模型都产生了波动和脱离。

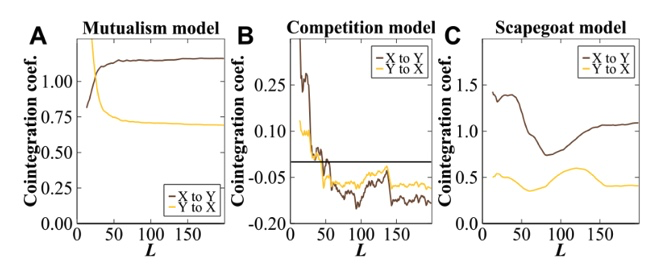
图15：共生、竞争、替罪羊的β系数

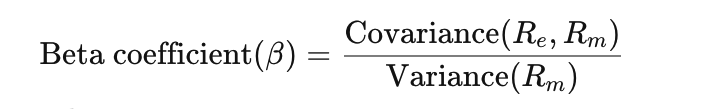
方法图：β系数考虑了某个变量Re相对整体Rm变动情况，为协方差和总收益方差之比

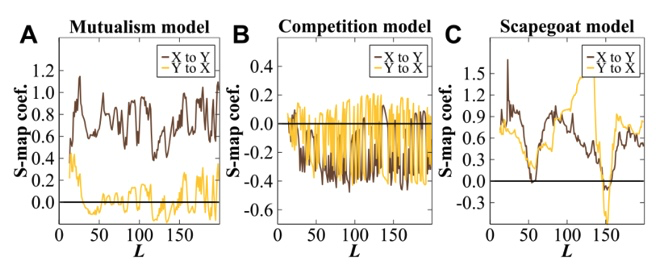
最后是 S-map（Sequential Locally Weighted Global Linear Maps）的结果，与收敛交叉映射（CCM）[16] 作为生态学分析种间竞争非线性数据建模主要方法之一。S-MAP 相当于一个局部加权的线性回归，考虑目标点在重构吸引子中邻域状态进行预测。CCM 以之为基础，通过考虑动力系统 M 在两个子空间 X 和 Y 延迟序列重构的相空间 Mx 和 My 之间相关性计算来确定因果关系。

但他们都没有像基于符号动力学的因果模式矩阵相空间重构法那样考虑每个点最近邻域本身的变化模式，并对所定义的几种因果模式进行分离。

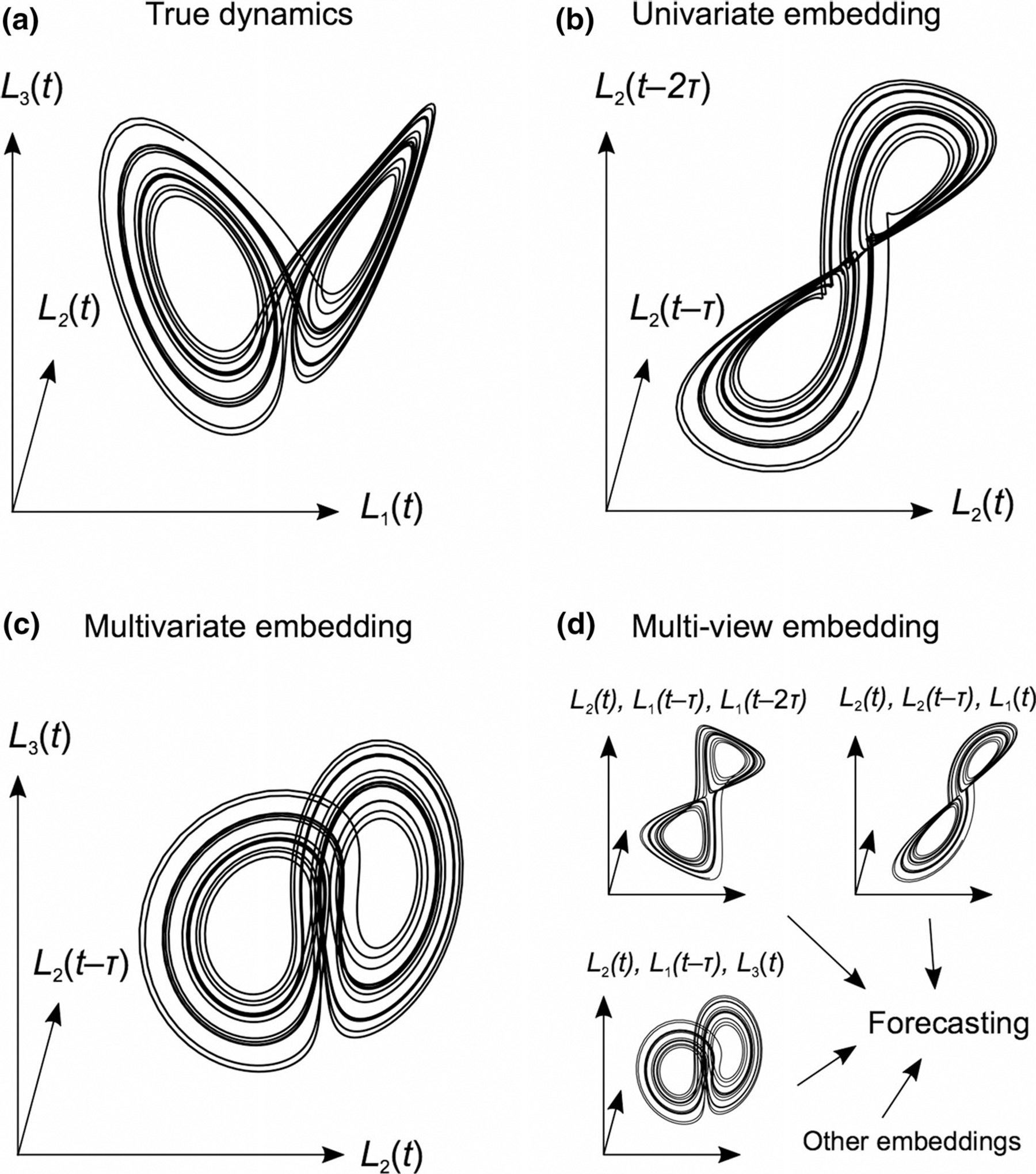
图16：方法图：几种单变量和多变量嵌入的 S-MAP 方法[17]

方法图：CCM 考虑了目标点在邻域变化情况，但没有考虑最近邻域本身的变化模式

可以看到 S-map的结果同样非常不稳定，尤其在 C 的替罪羊模型中，X→Y 和 Y→X 在不同时期交替出现，意味着 X、Y 之间没有稳定的关系。

上面方法之所以无法获得稳定而有意义结果的原因，就在于很难处理变量之间的不断变动的非线性因果关系。如果我们采取基于符号动力学的相空间重构方法，会得到以下结果：

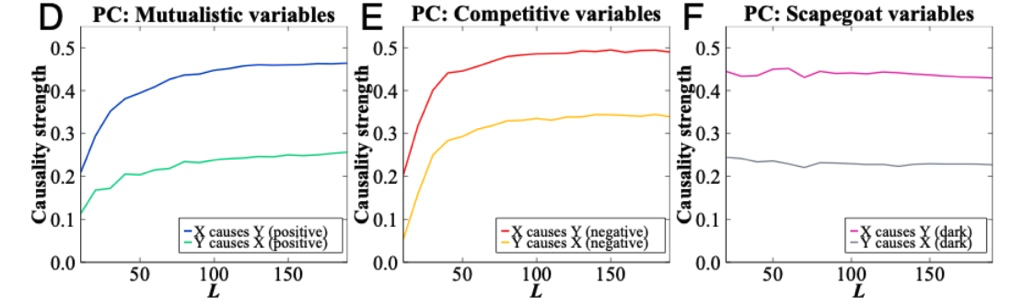
可以看到，清晰地分离出了主要的因果关系。在共生、竞争、替罪羊模型中，其主要作用的分别是 X→Y 的正向、负向、暗因果关系。

金融市场的例子

作者在两篇论文中，主要对主权国家的CDS金融市场进行了分析。数据来自 Thomson Reuters Datastream，计算了 69 个国家信用违约互换市场影响链接节点情况。

正向因果影响节点在大于 0.2，0.4，0.6 去除阈值以下节点情况如下：

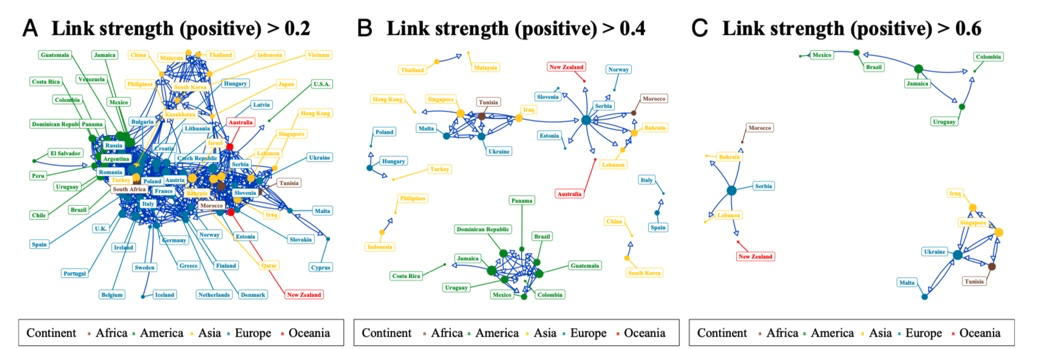
负向因果去除阈值以下节点情况如下：

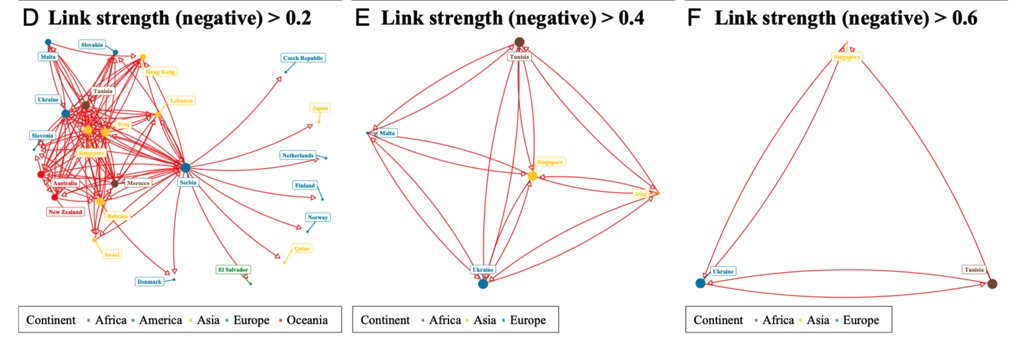
最后是暗因果去除阈值以下节点情况：

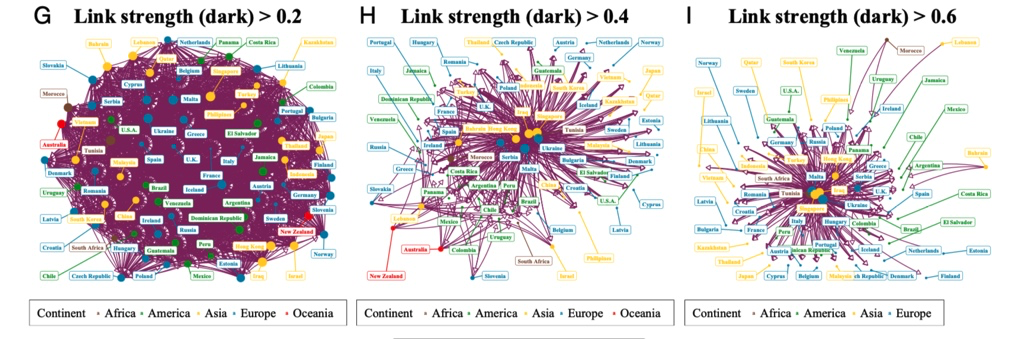
我们可以看到，在CDS金融市场总体因果模式中暗因果是最持久的类型，是它主导了市场本身。

作者认为，通过分析三种因果影响类型在复杂系统尤其是金融市场的比重，可以为国家和企业或个人投资决策提供最有效的决策依据，是一种“天赐的礼物”。

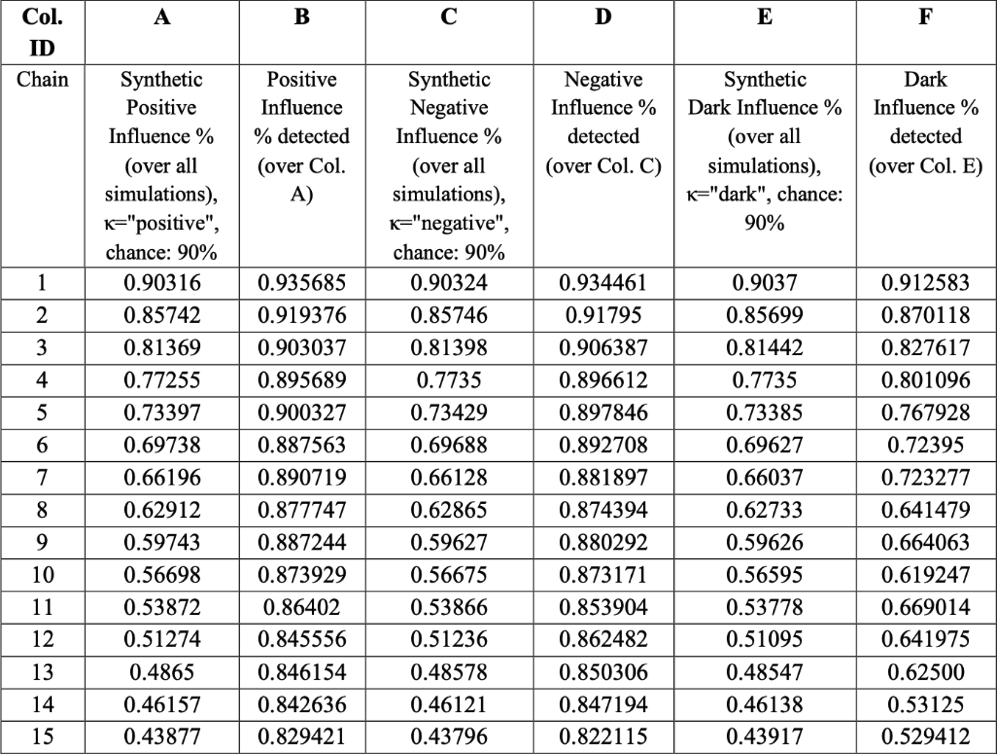
在下表中，作者们对三种原始模型数据（ACE）和三种实际数据预测（BDF）效果进行了评估，可以看到，对三种因果关系，单个链长准确度都超过 90%，而即使经过了十五个节点的链接，对系统数据依然有着 50%以上甚至 80%准确的反映。

其他模型的关系

在去年，马克斯·普朗克智能系统中心主任 Bernhard Schölkopf 写的一篇有关机器学习中的因果推断的综述中[18]，作者用一张表格总结了历来主流因果模型分类和特点。这几类模型并非都能从数据中习得（最右），但都能对独立同分布数据（IID）进行预测（左边）。

图17：因果模型种类：从 IID 中预测、在干预分布后预测、回答反事实、提供物理洞见、从数据中学习

机械物理模型：理想的动力学模型，通常以确定性的微分方程的形式呈现，最大优点是能清晰抽象物理实在关系。但也因此过于依赖人为数学建模而非数据驱动。

结构因果模型：能对具体物理事件抽象，又保留了对特定事件干和反事实问题的能力（通过对变量取特定值）。在采用确定性方程的 SCM 中，变量之间关系可以是非线性、连续的、互为因果的。

因果图：直观清晰，对离散具体事件建模，能够计算干预后结果分布（do 算子），但对比 SCM 不善于对反事实情况进行回答（图示方法的缺点）。

概率统计模型：主流机器学习方法，仅仅从独立同分布数据（IID）习得并进行预测，无法对建模副现象关联以外任何事提供见解。

然而所有这些模型，即使能表达非线性关系，例如宏观物理模型（前面的恋爱动力学和生态学理论模型）或结构因果模型，对过程性因果关系（特点是具备因果环路）处理往往都有一定条件和限制[18][20][21]，目前没有形成一个统一、有效地处理框架。

而基于时空邻域对相空间重构的符号动力学方法，无论对过程性因果，还是离散的事件性因果，都能提供一种分析非线性因果关系动力模式的有效方法。它继承了之前的一些研究，如CCM 的优点，可以扩大数据点到最近邻域集研究以提取多种因果模式，对非线性因果反馈环路模式也能进行有效分离和计算，无论是确定性方程分析，还是数据驱动的数据建模，都能为相应的复杂系统结构提供更好的理解并得到更有效的决策依据。

五. 因果之路走向何方

“因该果海，果彻因源” ——《大方广佛华严经》

对因果的探索绝不仅仅囿于因果本身，还可能关乎世界万物的实在，我们的主观意识和自由意志的意义。

在 Wolfram 今年最新计划「Finally We May Have a Path to the Fundamental Theory of Physics」[21]中，因果关系就处于一个隐蔽而重要的地位——正是因为所谓「因果不变性」的性质，我们才得以拥有一个有意义的客观世界。

相关阅读：

Wolfram长文全译：从简单规则到系统物理学

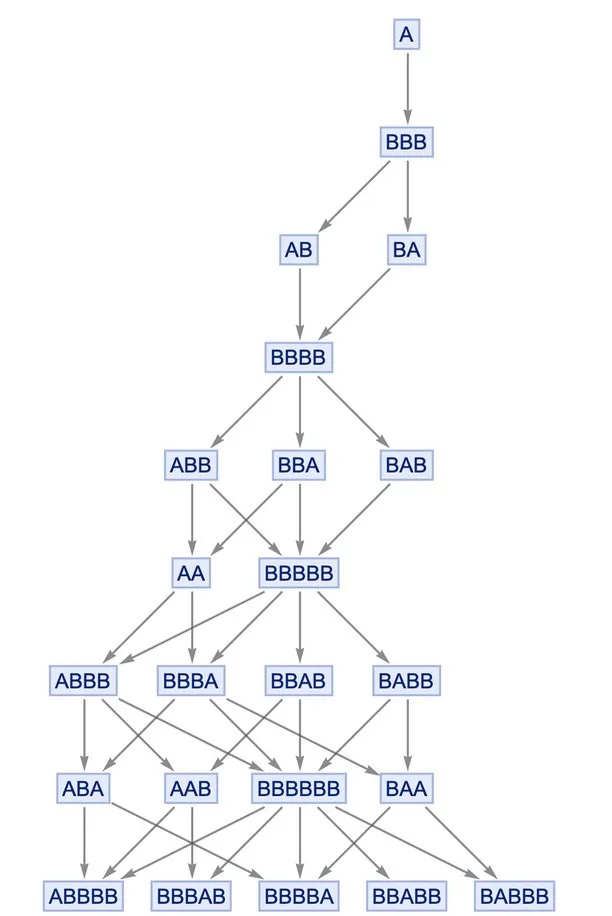
图18：因果不变性

假设我们有这样一条规则：{A → BBB, BB → A}，也就是说，对所有 A 都可以用 BBB 替换，对所有的 BB 都可以用 A 替换。这样我们就可以通过这个规则得到一个多路系统，绘制出一个“多路图"，显示可能发生的一切。然而即使生成分支存在的两条历史道路，在多元系统中分开了，它们也只需要一个步骤就会重新融合：即跟踪上面的图，你会发现这样的现象，生成的每一对分支总是随后合并，只需要再多走一步。

即使我们的宇宙和想象中最相似的可能世界发生的事件不同，“因果不变性”所体现的分支和合并之间平衡，依然保证了有意义客观现实存在。在我们熟知的广义相对论中，即使时空是相对的，然而依然有不变量存在，即时空构成的四维矢量（Four-vector），这其中就包括了事件在类时（timelike）间隔中的因果关系。

可以这样说，因果不变性和四维矢量不变量，保证了包括相对论和量子力学以及一切有意义科学理论客观性的存在——无论是哪种科学模型，是否是在更大的时空或因为主体能力限制被降格为近似，但那只是近似，并不代表是主观构建。

开始我们已经提到，是分析哲学尤其逻辑学的发展，有关反事实和模态逻辑的研究，在如今统计方法占统治地位的时候，让科学家们重新拾起对因果的信念和探索。而叔本华也从充足理由律四重根区分了逻辑推理和数学证明，与现实对象因果关系的不同。那么科学真理，或者说科学命题，与逻辑命题和数学命题之间究竟是一种什么关系呢？

以逻辑学来看，在因果不变性或因果有效的情况下，逻辑、数学、科学代表了三种不同真理，主要包括三种不同蕴涵（implication）关系：分别是逻辑蕴涵、形式蕴涵与实质蕴涵。

三种蕴涵之间关系，也就是三类真理之间的关系。按照模型论观点，对系统 L 的一个公式 A→B：

逻辑蕴涵：也叫严格蕴涵。 “A 严格蕴涵 B” 记为 A⊰B，代表在任意一个模型取值都真。也就说 “A 真 B 假”不仅是假的，而且是不可能的。每个模型是一个可能的世界，可见逻辑蕴涵在在所有可能的世界中为真。例子：“苏格拉底是人⊰ 苏格拉底是动物”。

形式蕴涵：是有关命题函项的，形式为 ∀x（φx→ψx），意为：对一切 x 而言，如果 φx 则 ψx。变元 x 每一次取值都可以看作一个可能世界，因此数学也是所有可能世界都为真的必然真理。只不过相对逻辑蕴涵，因为数学又与每个可能世界以及世界中主体存在结构耦合，因此仅仅通过数学研究就能得出有关世界必然且有意义的结论。例子：“任意一个素数，无论有多大，在相隔246以内一定存在另一个素数”。

实质蕴涵：即假言推理“如果 A，那么 B”，记 A→B。因为前件是假设的情境，故命题只在某个世界是正确的事实，而非在所有可能世界为真。可见包含实质蕴含的现实命题即反事实推理，通过寻找最相似世界反推我们世界的因果关系。因为科学也总是依赖于某些先验假设，作为不同的研究纲领，因此科学命题也只能在某种假设和语境下为真。当然根据 Wolfram 的因果不变性，所有有效的科学理论必然反映某种等价的客观现实，而非主观上任意构建。例子：“在忽略观察者的绝对时空下，牛顿定律成立”。

可见科学处理的因果关系主要就是逻辑中的实质蕴涵， 即物理世界客体事件之间的关系。它总是在某一时间、空间和语境下为真，而非像逻辑或数学那样的形式系统存在永真。但也正因为如此，科学研究总是和我们所处的环境相关，总是能随着我们的生存和认知边界不断修正更新，对我们所关注的事物做出最具指导性的结论。

科学命题之所以有局限，正因为我们宇宙的规律，让身在其中的我们受到必然的物理限制：

定域性因果：相对论条件下约束光速有限，这使得人类一切获取信息的手段都不超过以观察者为中心的“光锥”范围（“光锥之内就是命运”）。无论是观察还是干预，人类所做的改变只能在光锥之内，不可能再超越光锥传递因果关系。这就是相对论的定域性原则（Principle of locality）。至于量子纠缠那样的超距作用，因为不能传递有效的信息，实际同样无法产生超越光速的因果效应（违反会产生因果悖论）。

混沌系统的不确定性：混沌系统的初始敏感性，导致即使对初始位置和动量的测量有极其微小的不精确，也会导致对其的长期预测产生巨大的误差。这意味着任何图灵等价的设备都无法通过结果数据反推系统初始状态。

量子不确定性：量子力学中系统波函数的观察者效应，以及实际存在的图灵机读取数据势必会影响环境信息本身（这也是形式系统和物理系统的差别），会导致系统不可避免的语义信息损失。

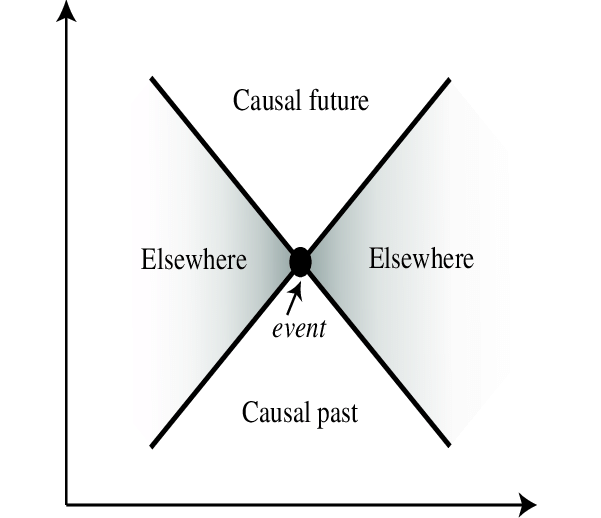
图19：一切影响现在的未来过去的因果关系都包裹在当前时间点的光锥中

由于以上限制，在处理经验世界因果关系时，我们不可能像逻辑或数学那样得到永真的科学定律。但即使如此，采取对物理世界进行干预，如控制实验，或者通过考虑模态世界的可能性，采用反事实推理，弥补现实的信息损失，我们还是能得到我们宇宙更强的因果关系的。

目前，有关因果在宇宙中的地位，物理学家们也一直在研究。在一类时空离散化假设下发展的方法中，一些物理学家认为宇宙的基本组成既不是空间也不是时间，而是更具本源性质的某种离散结构，例如量子比特、时空格点或因果关系。

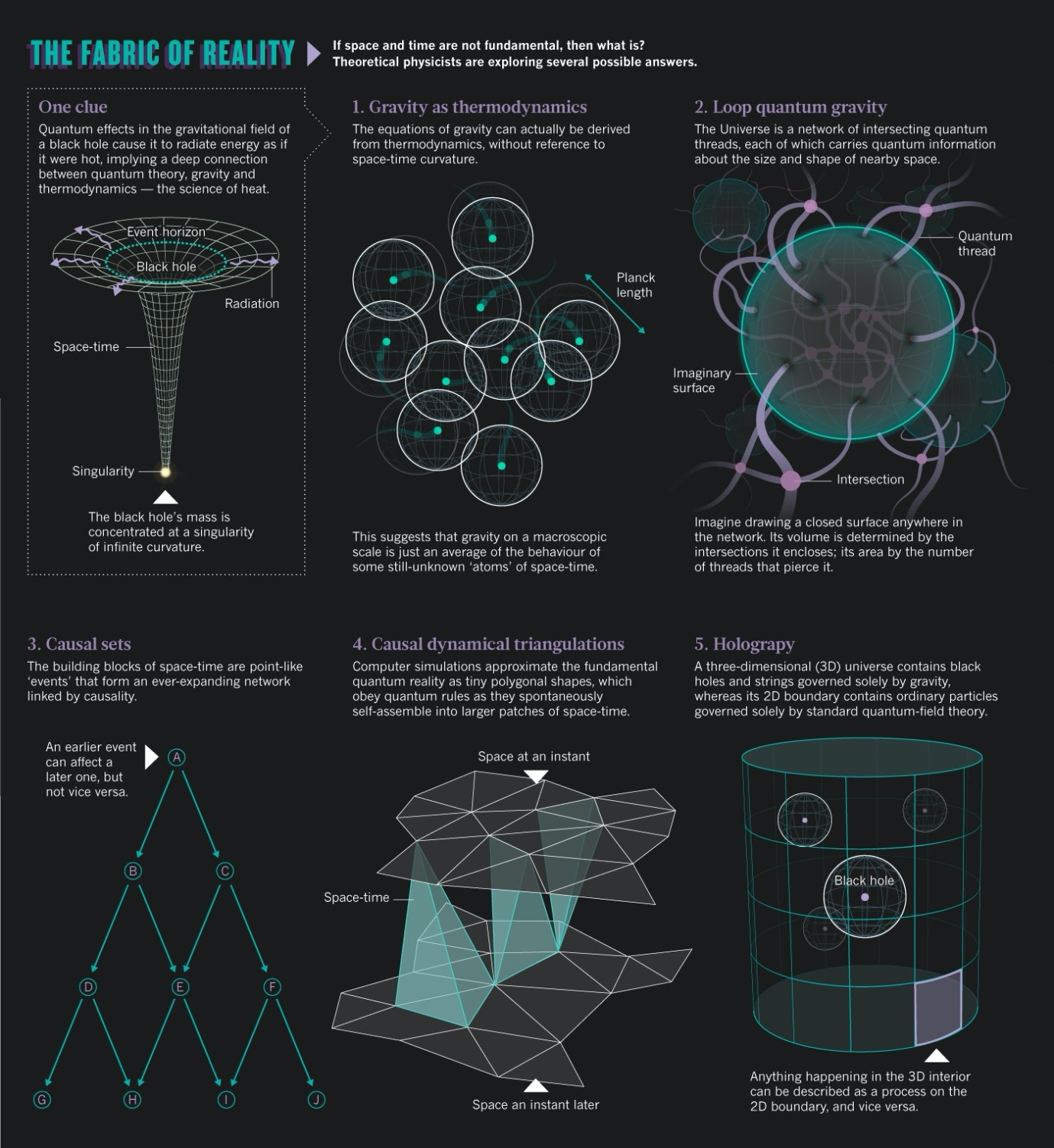
图20：几种候选物理学终极理论

其中与弦理论、圈量子理论、全息原理等理论一起作为终极理论的候选之一的因果集理论，就认为宇宙的基本组成是普朗克时空下一系列的物理事件，这些事件构成了因果集，事件之间的偏序关系描述了其中的因果。而对事件的描述，正如广义相对论中同时的相对性一样，不可避免地需要引入观测者所在的坐标系和参照系。

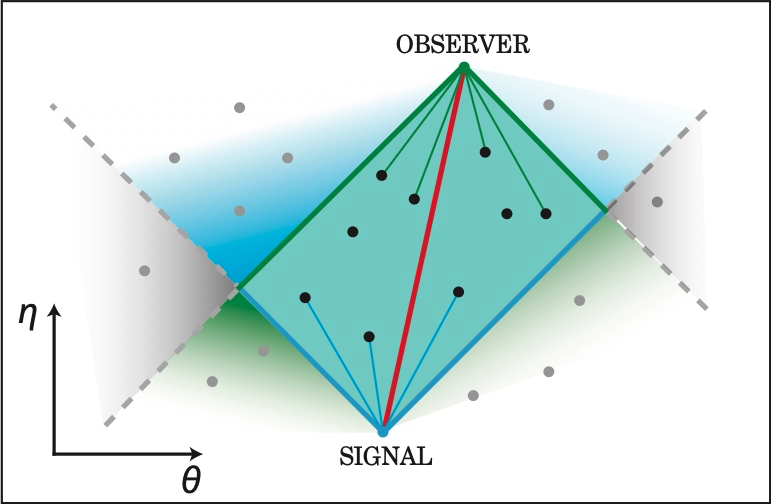
图21：在时空二维坐标（η ，θ）下， 因果集的事件元素以一定强度随机分布在特定时空区域，以共形45度直线绘制出的光锥，约束了每个事件过去和未来的因果。当一对元素（如绿和蓝）的光锥重叠、或由粗红线表示出时间分隔时，我们说事件之间具有因果关系。既作为信号的未来又作为观察者的过去的黑色元素，成对形成了以鸭绿色表示的 Alexandroff 集[23]

那么最终，因果之路后面会走向何方？我们能否跨越不确定性时代？

如果我们再次从哲学和逻辑学取经的话，也许下一次会走向基于情境理论的因果模型。

在上世纪八十年代，两位美国哲学家和逻辑学家乔恩・巴威斯和约翰・佩里在《情境与态度》（Situations and Attitudes）一书中，提出了有关因果关系的情景理论，开创了情境语义学研究。在其中因果关系要素既包括存在世界的具体部分（经验世界），将之称为“具体情境—殊型”，也包括非现实存在的“抽象情景-类型”（理念世界或模态世界），并且对二者抱有实在论态度。

巴威斯和佩里认为，如果一个对象被某个主体感知并被当做世界的一部分在看，那么主体所诉诸的事件就在某种场景中，在这种情况下，是一幅场景使得某些事件（语句）为真，某些事件（语句）为假，或使得另外一些语事件（语句）既不真又不一假——我们可以看到，在这个因果模型，引入了作为感知者或观察者的主体，主体所依仗的情景，由此决定在情景中的事件（语句）。在此因果关系中，事件（语句）的真假，就取决于与情景的关系——尤其，在这个因果模型中是三值的，可以为真，假，或没有定义。

美国哲学家罗伯特·C·孔斯（Robert C.Koons）在此基础上做了进一步研究，《重塑实在论》认为，有一个极大的事实或情景，就是我们的世界。如果对比暗因果模型，我们可以发现，情景对应时空邻域——命题与情景的关系，就是变量状态与最近邻域之间的关系。决定因果关系存在与否的不仅是事件状态本身，还包括情景或时空邻域的状态。而因果关系除了真值 T 和假值 F 外，还可以取未定义值 U ——我们可以视之为潜在的、在真假之间的因果关系即暗因果关系。

自然，当因果关系的效应为假，或者无法定义（计算）时呈现的暗因果，就是因为前面提到的身处这个宇宙的观察者我们所遭遇的物理硬性限制了。

但我们也可以看到，科学发展的历程，从确定性模型，到统计方法，到反事实推理和结构因果模型，最后到考虑时空邻域和情境，都是因为遭遇了更复杂的系统和更具体场景时，让我们不得不发展新方法去研究解决——而非发现整个宇宙真的越来越存在不确定性。是我们的需求以及对充足理由律的内在信念，促使我们去这样做，寻找规律，而不是听天由命，将一切归结为偶然。

并且，在这个过程中，我们并没有失去自由，因为因果不意味着完全确定。我们总能在尊重宇宙客观规律同时，做出我们自己的选择，让自己的主观融入宇宙客观的一部分。或者相反，我们的宇宙因为我们的选择、我们所创造出新的实在而变得更有生命。在冥冥中，这一切新的选择和创造都保存在了永恒的四维时空中——如果真有上帝视角的话。

图22：罗伯特·C·孔斯在《重塑实在论》建立的基于因果的万有理论

因果之路走向何方？

也许这个问题还是太难，现在还无法回答，也许我们永远无法找到所有原因。但不管走向何方，它绝对不会再走向不确定性，在不确定性中存在因果，这不仅是理论或信念，更是所有意识主体的一生的实践。

——不管可能世界是否真的存在，只要数学存在，逻辑存在，我们存在，对因果根源的探寻就会一直存在。我们终将知道，它是不是宇宙本身。